Functions
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::root () const
	Return the root of the suffix tree.
bool	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::is_leaf (node_type v) const
	Decide if a node is a leaf in the suffix tree.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::ith_leaf (size_type i) const
	Return the i-th leaf (1-based from left to right) of the suffix tree.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::depth (node_type v) const
	Returns the depth of node v.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::node_depth (node_type v) const
	Returns the node depth of node v.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::leaves_in_the_subtree (node_type v) const
	Calculate the number of leaves in the subtree rooted at node v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::leftmost_leaf_in_the_subtree (const node_type &v) const
	Calculates the leftmost leaf in the subtree rooted at node v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::rightmost_leaf_in_the_subtree (const node_type &v) const
	Calculates the rightmost leaf in the subtree rooted at node v.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::lb (const node_type &v) const
	Calculates the index of the leftmost leaf in the corresponding suffix array.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::rb (const node_type &v) const
	Calculates the index of the rightmost leaf in the corresponding suffix array.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::parent (node_type v) const
	Calculate the parent node of a node v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sibling (node_type v) const
	Returns the next sibling of node v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::child (node_type v, const unsigned char c, size_type &char_pos) const
	Get the child w of node v which edge label (v,w) starts with character c.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::child (node_type v, const unsigned char c)
	Get the child w of node v which edge label (v,w) starts with character c.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::ith_child (node_type v, size_type i) const
	Get the ith child of a node v.
unsigned char	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::edge (node_type v, size_type d) const
	Returns the d-th character (1-based indexing) of the edge-label pointing to v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::lca (node_type v, node_type w) const
	Calculate the lowest common ancestor (lca) of two nodes v and w of the suffix tree.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sl (node_type v) const
	Compute the suffix link of node v.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::wl (node_type v, const unsigned char c) const
	Compute the Weiner link of node v and character c.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sn (node_type v) const
	Compute the suffix number of a leaf node v.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::id (node_type v) const
	Computes a unique identification number for a node of the suffix tree in the range [0..nodes()-1].
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::inv_id (size_type id)
	Computes the node for such that id(v)=id.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::nodes () const
	Get the number of nodes of the suffix tree.
node_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::node (size_type lb, size_type rb, size_type l=0) const
	Get the node in the suffix tree which corresponds to the lcp-interval [lb..rb].
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::degree (node_type v) const
	Get the number of children of a node v.
size_type	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::tlcp_idx (size_type i) const
	Maps an index i to the position in TLCP where LCP[i] can be found.
void	sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::print_info () const
	Print some infos about the size of the compressed suffix tree.

Function Documentation

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::degree ( node_type v ) const [inline]

Get the number of children of a node v.

Parameters:

v	A valid node v of a cst_sada.

Returns:: The number of children of node v.

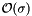
Time complexity: $\Order{\sigma}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::depth ( node_type v ) const [inline]

Returns the depth of node v.

Parameters:

v	A valid node of the suffix tree.

Returns:: The depth of the node.

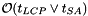
Time complexity: $\Order{\lcpaccess \vee \saaccess}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

unsigned char sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::edge	(	node_type	v,
		size_type	d
	)		const `[inline]`

Returns the d-th character (1-based indexing) of the edge-label pointing to v.

Parameters:

v	The node at which the edge path ends.
d	The position (1-based indexing) of the requested character on the edge path from the root to v. 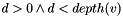$d > 0 \wedge d < depth(v)$

Returns:: The character at position d on the edge path from the root to v.

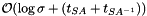
Time complexity: $\Order{ \log\sigma + (\saaccess+\isaaccess) }$

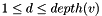
Precondition:: $1 \leq d \leq depth(v)$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::id ( node_type v ) const [inline]

Computes a unique identification number for a node of the suffix tree in the range [0..nodes()-1].

   \param v A valid node of a cst_sada.

Returns:: A unique identification number for the node v in the range [0..nodes()-1]

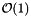
Time complexity: $\Order{1}$

See also:: inv_id(size_type id)

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::inv_id ( size_type id ) [inline]

Computes the node for such that id(v)=id.

   \param id An id in the range [0..nodes()-1].

Returns:: A node v of the CST such that id(v)=id.

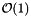Time complexity: $\Order{1}$ for leaves and 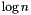$\log n$ for inner nodes

See also:: id(node_type v)

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

bool sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::is_leaf ( node_type v ) const [inline]

Decide if a node is a leaf in the suffix tree.

Parameters:

v	A valid node of a cst_sada.

Returns:: A boolean value indicating if v is a leaf.

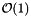
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::ith_child	(	node_type	v,
		size_type	i
	)		const `[inline]`

Get the ith child of a node v.

   \param v A valid tree node of the cst.

Parameters:

i	1-based Index of the child which should be returned. 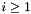$i \geq 1$ .

Returns:: The i-th child node of v or root() if v has no i-th child.

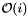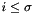
Time complexity: $\Order{i}$ for $i \leq \sigma$

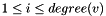
Precondition:: $1 \leq i \leq degree(v)$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::ith_leaf ( size_type i ) const [inline]

Return the i-th leaf (1-based from left to right) of the suffix tree.

Parameters:

i	1-based position of the leaf. 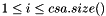$1\leq i\leq csa.size()$ .

Returns:: The i-th leave.

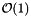
Time complexity: $\Order{1}$

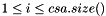
Precondition:: $1 \leq i \leq csa.size()$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::lb ( const node_type & v ) const [inline]

Calculates the index of the leftmost leaf in the corresponding suffix array.

Parameters:

v	A valid node of the suffix tree.

Returns:: The index of the leftmost leaf in the corresponding suffix array.

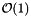
Time complexity: $\Order{1}$

Note: lb is an abbreviation for ,,left bound''

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::lca	(	node_type	v,
		node_type	w
	)		const `[inline]`

Calculate the lowest common ancestor (lca) of two nodes v and w of the suffix tree.

Parameters:

v	The first node for which the lca with the second node should be computed.
w	The second node for which the lca with the first node should be computed.

Returns:: A node that is the lowest common ancestor of v and w in the suffix tree.

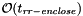
Time complexity: $\Order{\rrenclose}\$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::leaves_in_the_subtree ( node_type v ) const [inline]

Calculate the number of leaves in the subtree rooted at node v.

Parameters:

v	A valid node of the suffix tree.

Returns:: The number of leaves in the subtree rooted at node v.

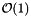
Time complexity: $\Order{1}$

This method is used e.g. in the algorithm::count method.

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::leftmost_leaf_in_the_subtree ( const node_type & v ) const [inline]

Calculates the leftmost leaf in the subtree rooted at node v.

Parameters:

v	A valid node of the suffix tree.

Returns:: The leftmost leaf in the subtree rooted at node v.

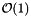
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::node_depth ( node_type v ) const [inline]

Returns the node depth of node v.

Parameters:

v	A valid node of a cst_sada.

Returns:: The node depth of node v.

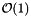
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::parent ( node_type v ) const [inline]

Calculate the parent node of a node v.

Parameters:

v	A valid node of the suffix tree.

Returns:: The parent node of v or root() if v equals root().

Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::rb ( const node_type & v ) const [inline]

Calculates the index of the rightmost leaf in the corresponding suffix array.

Parameters:

v	A valid node of the suffix tree.

Returns:: The index of the rightmost leaf in the corresponding suffix array.

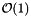
Time complexity: $\Order{1}$

Note: rb is an abbreviation for ,,right bound''

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::rightmost_leaf_in_the_subtree ( const node_type & v ) const [inline]

Calculates the rightmost leaf in the subtree rooted at node v.

Parameters:

v	A valid node of the suffix tree.

Returns:: The rightmost leaf in the subtree rooted at node v.

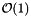
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::root ( ) const [inline]

Return the root of the suffix tree.

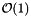
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sibling ( node_type v ) const [inline]

Returns the next sibling of node v.

Parameters:

v	A valid node v of the suffix tree.

Returns:: The next (right) sibling of node v or root() if v has no next (right) sibling.

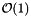
Time complexity: $\Order{1}$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

node_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sl ( node_type v ) const [inline]

Compute the suffix link of node v.

Parameters:

v	A valid node of a cst_sada.

Returns:: The suffix link of node v.

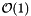
Time complexity: $\Order{ 1 }$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::sn ( node_type v ) const [inline]

Compute the suffix number of a leaf node v.

Parameters:

v	A valid leaf node of a cst_sada.

Returns:: The suffix array value corresponding to the leaf node v.

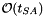
Time complexity: $\Order{ \saaccess }$

template<class Csa = csa_sada<>, class Lcp = lcp_support_sada<>, class Bp_support = bp_support_sada<>, class Rank_support10 = rank_support_v<10,2>, class Select_support10 = select_support_mcl<10,2>>

size_type sdsl::cst_sada< Csa, Lcp, Bp_support, Rank_support10, Select_support10 >::tlcp_idx ( size_type i ) const [inline]

Maps an index i to the position in TLCP where LCP[i] can be found.

Parameters:

i	The index in the LCP array

Returns:: The corresponding position in the TLCP array

Functions

Function Documentation