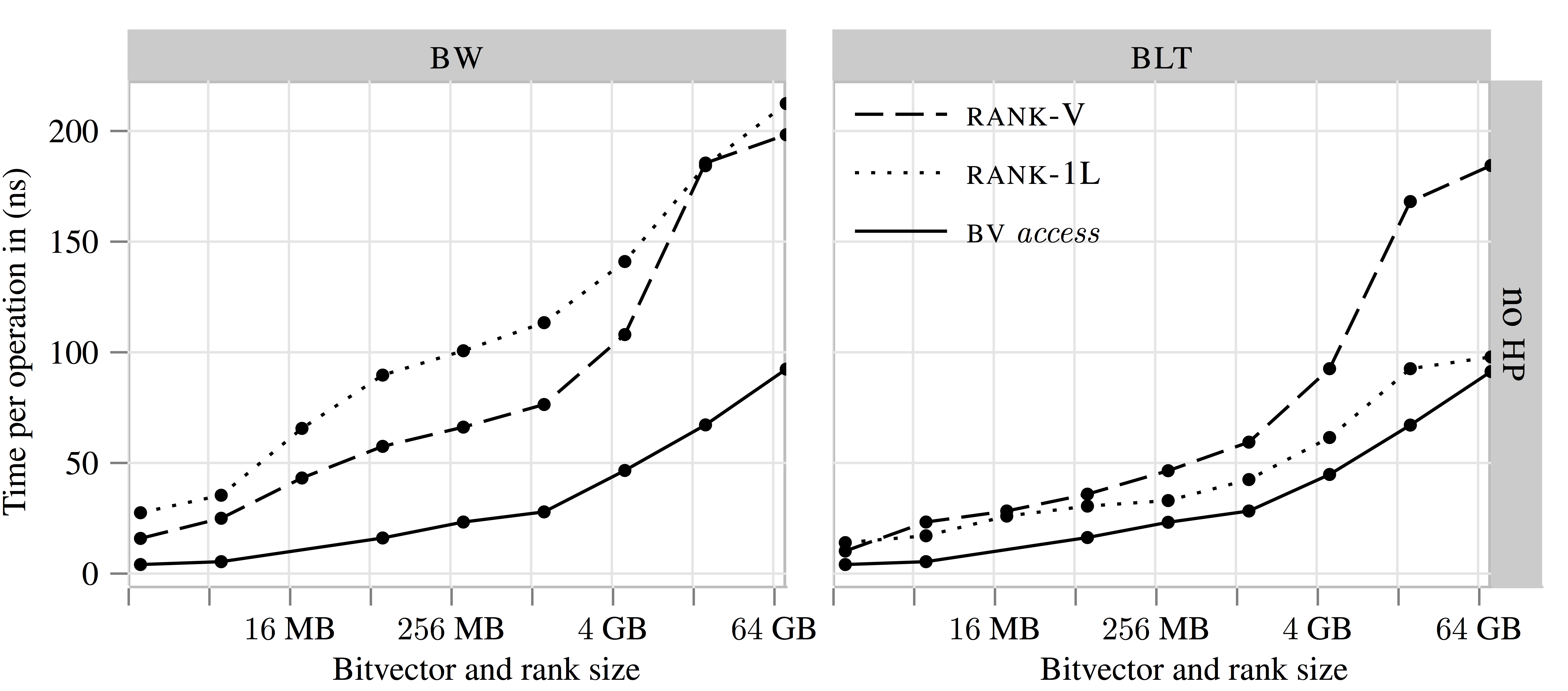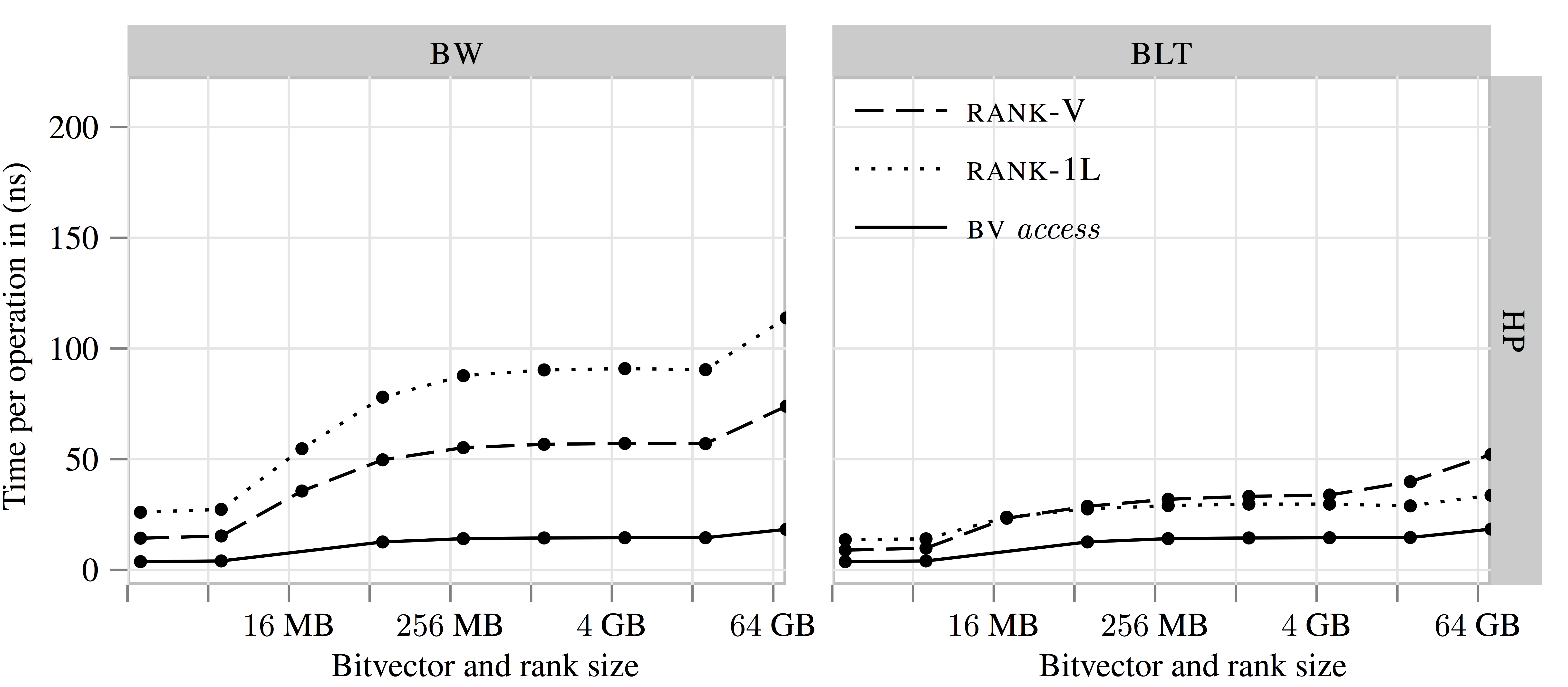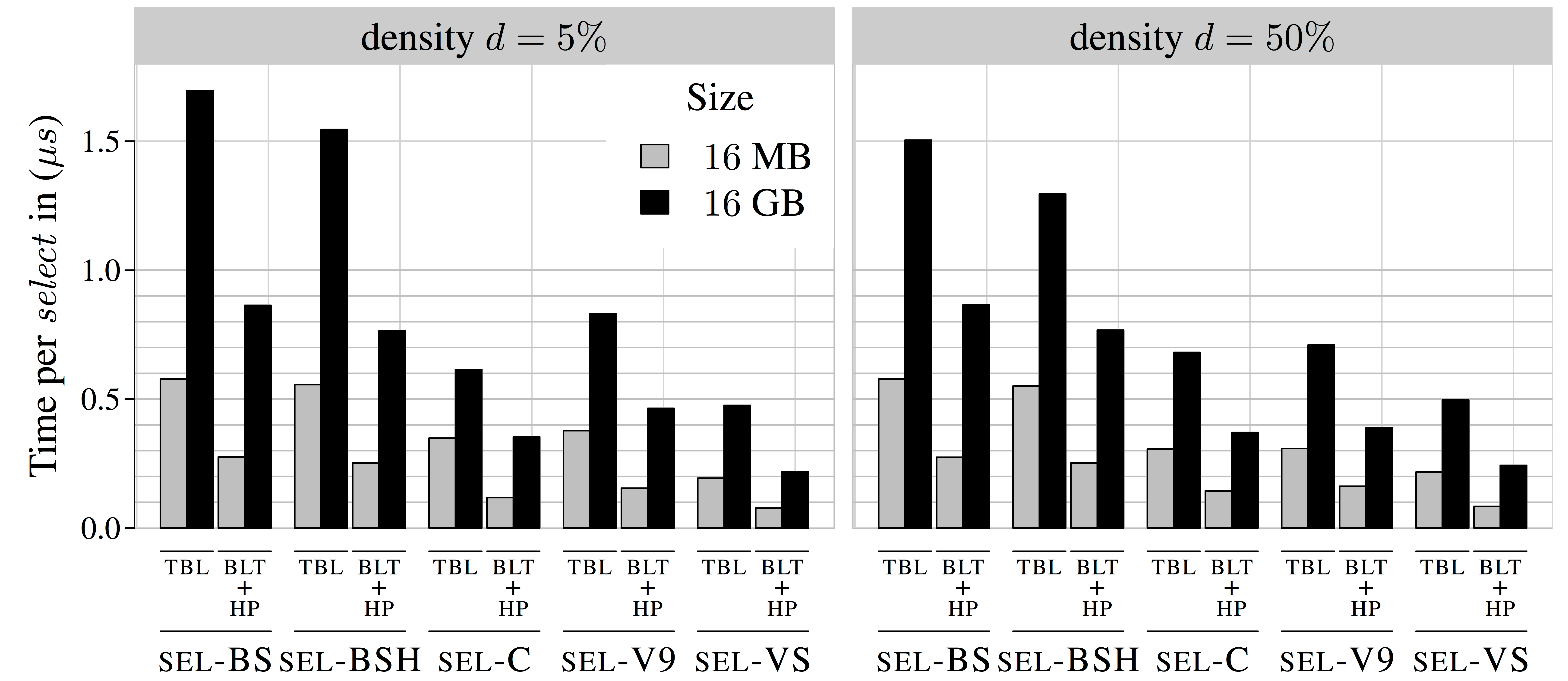Goal: Provide an easy-to-use, highly-efficient, configurable, and extensible library of succinct data structures for researchers and practitioners.

It is/was a challenge to meet all this goals. Here is the current state:

• C++ is used (great for resource-constraint programming).
• Templates are used to make it configurable.
• STL concepts are used to make it easy-to-use.
• Space and time efficient construction using the semi-external approach.
• Construction is configurable between in-memory and semi-external.
• All indexes support byte and integer sequences.
• Implements highlights of 40 research articles.

Development by Timo Beller, Matthias Petri, me, and others.

• Get the source code
   

  git clone https://github.com/simongog/sdsl-lite.git
  

• Install the include and library files into SDSL_INSTALL_PATH
  (default value is $HOME)
   

  cd sdsl-lite
  ./install.sh SDSL_INSTALL_PATH
  

• Lets compile* the tutorial programs
   

  cd tutorial
  make
  

#include <iostream>
#include <sdsl/vectors.hpp>

using namespace std;
using namespace sdsl;

int main(){
    int_vector<> v = {3,2,1,0,2,1,3,4,1,1,1,3,2,3};
    v[1]=0;
    util::bit_compress(v);
    cout << v << endl;
    cout << size_in_bytes(v) << endl; 
}

Output:

3 0 1 0 2 1 3 4 1 1 1 3 2 3
17

enc_vector<> = apply self-delimiting code on deltas

int_vector<> v(10*(1<<20));
for (size_t i=0; i<10; ++i)
    for (size_t j=0; j<1U<<20; ++j)
        v[i*(1<<20)+j] = j;
cout << size_in_mega_bytes(v) << endl;
util::bit_compress(v);
cout << size_in_mega_bytes(v) << endl;
enc_vector<> ev(v);
cout << size_in_mega_bytes(ev) << endl;

Output:

80
25
1.70902

vlc_vector<> = apply self-delimiting code on elements

 
// initialize vector with 10 mega zeros
int_vector<> v(10*(1<<20), 0);
v[0] = 1ULL<<63;
util::bit_compress(v);
cout << size_in_mega_bytes(v) << endl;
vlc_vector<> vv(v);
cout << size_in_mega_bytes(vv) << endl;

Output:

80
1.48442

 
#include <iostream>
#include <sdsl/bit_vectors.hpp>
using namespace std;
using namespace sdsl;

int main(){
    bit_vector b = {1,1,0,1,0,0,1};
    cout << b << endl;
    b = bit_vector(80*(1<<20), 0);
    for (size_t i=0; i < b.size(); i+=100)
        b[i] = 1;
    cout << size_in_mega_bytes(b) << endl;
}

1101001
10

Use rrr_vector<63> or sd_vector<> to represent compressible bitvectors

bit_vector b = bit_vector(80*(1<<20), 0);
for (size_t i=0; i < b.size(); i+=100)
    b[i] = 1;
cout << size_in_mega_bytes(b) << endl;
rrr_vector<63> rrrb(b);
cout << size_in_mega_bytes(rrrb) << endl;
sd_vector<> sdb(b);
cout << size_in_mega_bytes(sdb) << endl;

Output:

10
1.77071
0.987351

write_structure<JSON_FORMAT> can be used with every SDSL object and writes a space-breakdown into a stream

write_structure<JSON_FORMAT>(sdb, cout);

Any SDSL object o can be stored to or loaded from a file named file by method

Example:

    bit_vector<> b(10000000, 0);
    b[b.size()/2] = 1;
    sd_vector<> sdb(b);
    store_to_file(sdb, "sdb.sdsl");
    sdb = sd_vector<>();
    cout << sdb.size() << endl; // 0
    load_from_file(sdb, "sdb.sdsl");
    cout << sdb.size() << endl; // 10000000 

A support object holds a pointer to the supported object and adds functionality. E.g. rank_support_* structures add the rank operation to bitvectors.

bit_vector b = bit_vector(8000, 0);
for (size_t i=0; i < b.size(); i+=100)
    b[i] = 1;
rank_support_v<1> b_rank(&b); // <- pointer to b
for (size_t i=0; i<=b.size(); i+= b.size()/4) 
    cout << "(" << i << ", " << b_rank(i) << ") ";  

Output:

(0, 0) (2000, 20) (4000, 40) (6000, 60) (8000, 80)

Each bitvector class provides default types for rank supports.

sd_vector<> sdb(b);
sd_vector<>::rank_1_type sdb_rank(&sdb);
for (size_t i=0; i<=b.size(); i+= b.size()/4) 
    cout << "(" << i << ", " << sdb_rank(i) << ") ";
cout << endl;
rrr_vector<> rrrb(b);
rrr_vector<>::rank_1_type rrrb_rank(&rrrb);
for (size_t i=0; i<=b.size(); i+= b.size()/4) 
    cout << "(" << i << ", " << rrrb_rank(i) << ") ";

Output:

(0, 0) (2000, 20) (4000, 40) (6000, 60) (8000, 80)
(0, 0) (2000, 20) (4000, 40) (6000, 60) (8000, 80)

It is possible to generate rank structures for bit-patterns up to length 2 for bit_vector.

bit_vector b = {0,1,0,1};
rank_support_v<1> b_r1(&b);     // <- bitpattern `1` of len 1
rank_support_v<0> b_r0(&b);     // <- bitpattern `0` of len 1
rank_support_v<10,2> b_r10(&b); // <- bitpattern `10` of len 2
rank_support_v<01,2> b_r01(&b); // <- bitpattern `01` of len 2
for (size_t i=0; i<=b.size(); ++i)
    cout << i << ": "<< b_r1(i) << " " << b_r0(i)
         << " " << b_r10(i) << " " << b_r01(i) << endl; 

Output:

0: 0 0 0 0
1: 0 1 0 0
2: 1 1 0 1
3: 1 2 1 1
4: 2 2 1 2

Select structures can be used analogously.

bit_vector b = {0,1,0,1,1,1,0,0,0,1,1};
size_t zeros = rank_support_v<0>(&b)(b.size());
bit_vector::select_0_type b_sel(&b);

for (size_t i=1; i <= zeros; ++i)
   cout << b_sel(i) << " ";

Output:

0 2 6 7 8 

Select on a bit_vector can also be done for bit patterns of length 2.

bit_vector b = {0,1,0,1,1,1,0,0,0,1,1};
size_t cnt10 = rank_support_v<10,2>(&b)(b.size());
select_support_mcl<10,2> b_sel10(&b);

for (size_t i=1; i <= cnt10; ++i)
   cout << b_sel10(i) << " ";

Output:

2 6

Selecting works also on compressed bitvectors (sd_vector<> and rrr_vector<>)

sd_vector<> sd_b = bit_vector{1,0,1,1,1,0,1,1,0,0,1,0,0,1};
size_t ones = sd_vector<>::rank_1_type(&sd_b)(sd_b.size()); 
sd_vector<>::select_1_type sdb_sel(&sd_b);

cout << sd_b << endl;

for (size_t i=1; i <= ones; ++i)
    cout << sdb_sel(i) << " ";

Output:

10111011001001
0 2 3 4 6 7 10 13

Time performance of a single access/rank/select operation depends on

• Basic rank operation on 64-bit word:
  • BW: SWAR (SIMD Within A Register)
  • BLT: use popcount CPU instruction
 
• Virtual address space translation:
  • no HP: Use standard 4 kiB pages
  • HP: Use 1GiB pages (hugepages)
 
• Data structure design:
  • RANK-V: rank_support_v<> 25% overhead on top of bit_vector
  • RANK-1L interleaving bitvector data and rank data (bit_vector_il<>)

"BV access" is the baseline of accessing a random bit of a bit_vector.

"BV access" is the baseline of accessing a random bit of a bit_vector.

Performance of binary search select (SEL-BS*), select_support_mcl<> (SEL-C) and Vigna's solutions in Sux SEL-V9 and SEL-VS

Space breakdown for rrr_vector<K> with varying block size.

Runtime for rrr_vector<K> with varying block size.

• wt_pc<..>: Prefix code wavelet tree (parametrizable with shape, bitvector, rank, selects, alphabet) using . Shape specializations:
• wt_blcd<..>: Balanced-shaped WT
• wt_huff<..>: Huffman-shaped WT
• wt_hutu<..>: Hu-Tucker-shaped WT
• wt_int<..>: Balanced-shaped WT for large alphabets (parametrizable with bitvector, rank, selects)
• wt_rlmn<..>: Run-length WT (parametrizable with bitvector, rank, select, and the underlying WT)

Note:

• wt_pc and wt_rlmn can be parametrize to work on byte or integer alphabets.
• wt_blcd, wt_hutu and wt_int are order preserving WTs.

Any wavelet tree provides methods access (operator[]), rank(i,c), select(i,c), and inverse_select(i). Snippet of expl-13.cpp:

wt_blcd<> wt;
construct(wt, "expl-13.cpp", 1);
for (size_t i=0; i < wt.size() and wt[i]!='\n'; ++i) 
    cout << wt[i];
cout << endl;
cout << "number of lines  : " << wt.rank(wt.size(), '\n') << endl;
cout << "first '=' in line: " << wt.rank(wt.select(1, '='),'\n')+1 << endl;

Output:

#include <sdsl/wavelet_trees.hpp>
number of lines  : 15
first '=' in line: 10

Any WT-,CSA-, or CST-object o can be build for a file by calling
construct(o, file, num_bytes=0).

num_bytes specifies how the file should be interpreted:

More about construct(o, file, num_bytes):

• Semi-external construction (streams to and from disk) is space and time-efficient
• It's easy to use: YGWYD: You Get What You Declare.

For small object going to disk is a waste of time. Therefore:

Any WT-,CSA-, or CST-object o can be build in memory for a sequence data by

construct_im(o, data, num_bytes=0).

Build a byte-alphabet Hu-Tucker-shaped WT (order preserving) for a byte sequence.

    wt_hutu<rrr_vector<63>> wt;
    construct_im(wt, "こんにちは世界", 1);
    for (size_t i=0; i < wt.size(); ++i) cout << wt[i]; cout << endl;
    auto t1 = wt.lex_count(0, wt.size(), 0x80);   
    auto t2 = wt.lex_count(0, wt.size(), 0xbf);   
    cout << "# of chars        : " << wt.size() << endl;
    cout << "# of UTF-8 symbols: " << get<1>(t1)+get<2>(t2) << endl;

Output:

こんにちは世界
# of bytes        : 21
# of UTF-8 symbols: 7

Build an integer-alphabet balanced WT (order preserving) for a integer sequence and do a range search (index range = [1..5], value range=[4..8]).

    wt_int<rrr_vector<63>> wt;
    construct_im(wt, "6   1000 1 4 7 3   18 6 3", 'd');
    auto res = wt.range_search_2d(1, 5, 4, 18);
    for ( auto point : res.second )
        cout << point << " ";
    cout << endl;

Output (index/value pairs):

(3,4) (4,7) 

Build an integer-alphabet Huffman-shaped WT for an int_vector<> in memory and execute inverse_select.

    wt_huff_int<rrr_vector<63>> wt;
    construct_im(wt, int_vector<>({1981, 1974, 1990, 1974, 2014, 1974}));
    cout << "wt.sigma : " << wt.sigma << endl;
    cout << wt << endl;
    size_t idx = 5;
    auto r_c = wt.inverse_select(idx);
    cout << get<0>(r_c)+1 << " occurrence(s) of "
         << get<1>(r_c) << " in [0.." << idx << "]" << endl;

Output:

wt.sigma : 4
1981 1974 1990 1974 2014 1974
3 occurrence(s) of 1974 in [0..5]

Any CSA provides the access method (operator[]) and the following members:

• psi, lf,    isa, bwt, text,    L, F,    C, char2comp, comp2char

There are three CSA types:

SA and ISA sampling density, alphabet strategy and the SA value sampling strategy can be specified via template arguments.

Build an byte-alphabet CSA in memory (0-symbol is appended!). Output size, alphabet size, and extracted text in [0..csa.size()-1].

csa_bitcompressed<> csa;
construct_im(csa, "abracadabra", 1);
cout << "csa.size(): " << csa.size() << endl;
cout << "csa.sigma : " << csa.sigma << endl;
cout << csa << endl;  // output CSA
cout << extract(csa, 0, csa.size()-1) << endl;

Output:

csa.size(): 12
csa.sigma : 6
11 10 7 0 3 5 8 1 4 6 9 2
abracadabra

Do count and locate on a CSA constructed from a file. Snippet of expl-18.cpp:

    csa_wt<wt_huff<rrr_vector<63>>,4,8> csa; // 接尾辞配列
    construct(csa, "expl-18.cpp", 1);
    cout << "count(\"配列\") : " << count(csa, "配列") << endl;    
    auto occs = locate(csa, "\n");
    sort(occs.begin(), occs.end());
    auto max_line_length = occs[0];
    for (size_t i=1; i < occs.size(); ++i)
        max_line_length = std::max(max_line_length, occs[i]-occs[i-1]+1);
    cout << "max line length : " << max_line_length << endl;

Output:

count("配列") : 3 
max line length : 75

Formatted output of CSAs/CSTs using the csXprintf:

csa_wt<wt_int<rrr_vector<63>>> csa; 
construct_im(csa, "1 8 15 23 1 8 23 11 8", 'd');
cout << " i SA ISA PSI LF BWT   T[SA[i]..SA[i]-1]" << endl;
csXprintf(cout, "%2I %2S %3s %3P %2p %3B   %:3T", csa); 

Output:

 i SA ISA PSI LF BWT   T[SA[i]..SA[i]-1]
 0  9   1   1  3   8     0  1  8 15 23  1  8 23 11  8
 1  0   4   4  0   0     1  8 15 23  1  8 23 11  8  0
 2  4   7   5  8  23     1  8 23 11  8  0  1  8 15 23
 3  8   8   0  6  11     8  0  1  8 15 23  1  8 23 11
 4  1   2   7  1   1     8 15 23  1  8 23 11  8  0  1
 5  5   5   9  2   1     8 23 11  8  0  1  8 15 23  1
 6  7   9   3  9  23    11  8  0  1  8 15 23  1  8 23
 7  2   6   8  4   8    15 23  1  8 23 11  8  0  1  8
 8  3   3   2  7  15    23  1  8 23 11  8  0  1  8 15
 9  6   0   6  5   8    23 11  8  0  1  8 15 23  1  8

Configurable benchmark code facilitates

• reproducibility
• performance measurement on your hardware
• exploring different dimensions (input types, index types, compile flags,...)

SDSL includes a set of configurable benchmarks, which are very easy to execute. One example:

 cd benchmark/indexing_locate
 make timing

• SA is constructed in-memory. Used implementations:
  • Yuta Mori's libdivsufsort for byte alphabets
  • N. Jesper Larsson's qsufsort for integer alphabets
• Following construction steps are implemented semi-external using the int_vector_buffer<..> to stream data from and to disk.

It is very easy to keep track of memory resources allocated during the construction:

memory_monitor::start();
csa_wt<> csa;
construct(csa, "english.200MB", 1);
memory_monitor::stop();
memory_monitor::write_memory_log<HTML_FORMAT>(cout);

Steps for csa_wt<>: Load text, construct SA, construct BWT, construct WT, sample SA, sample ISA.

Any CST contains members csa and lcp and provides the following methods:

• nodes(), root(), begin(), end(), begin_bottom_up(), end_bottom_up()
• size(v), is_leaf(v), degree(v), depth(v), node_depth(v), edge(v,d), lb(v), rb(v), id(v), inv_id(i), sn(v)
• select_leaf(i), node(lb,rb)
• parent(v), sibling(v), lca(v,w), select_child(v,i), child(v,c), sl(v), wl(v,c), leftmost_leaf(v), rightmost_leaf(v)

There are two CST types:

The underlying CSA, LCP array and the balanced parentheses structure can be specified via template arguments.

Create the suffix tree of the overview slide, navigate to a node $v$ (first child of the node whose label starts with 'u'), and extract $v$'s node label.

cst_sct3<> cst;
construct_im(cst, "umulmundumulmum", 1);
cout << "inner nodes : " << cst.nodes() - cst.csa.size() << endl;
auto v = cst.select_child(cst.child(cst.root(), 'u'),1);
auto d = cst.depth(v);
cout << "v : " << d << "-[" << cst.lb(v) << "," << cst.rb(v) << "]" << endl;
cout << "extract(cst, v) : " << extract(cst, v) << endl;

Output:

inner nodes : 9
v : 4-[10,11]
extract(cst, v) : ulmu

Use a CSTs to calculate the $k$-th order entropy of a integer sequence.

cst_sct3<csa_wt<wt_int<rrr_vector<>>>> cst;
int_vector<> data(100000, 0, 10);
for (size_t i=0; i < data.size(); ++i)
    data[i] = 1 + rand()%1023;
construct_im(cst, data);
cout << "cst.csa.sigma: " << cst.csa.sigma << endl;
for (size_t k=0; k<3; ++k)
    cout << "H" << k << " : " <<  get<0>(Hk(cst, k)) << endl;

Output:

cst.csa.sigma: 1024
H0(data) : 9.99038
H1(data) : 6.52515
H2(data) : 0.0940461

The size of a CST depends heavily on the size of the underlying LCP array

cst_sct3<csa_wt<wt_huff<rrr_vector<>>>, lcp_support_sada<>> cst1;
construct(cst1, "english.200MB", 1);
cout << "cst1.lcp in MiB : " << size_in_mega_bytes(cst1.lcp) << endl;
util::clear(cst1);
cst_sct3<csa_wt<wt_huff<rrr_vector<>>>, lcp_dac<>> cst2;
construct(cst2, "english.200MB", 1);
cout << "cst2.lcp in MiB : " << size_in_mega_bytes(cst2.lcp) << endl;

Output:

cst1.lcp in MiB : 55.9235
cst2.lcp in MiB : 214.979

LCP structures provide the following methods: access (operator[]), size(), begin(),end(). There are eight types in SDSL:

Typical runtime for random accessing LCP structures (using csa_wt<wt_huff<>,32,32> as CSA and $s_{\mbox{LCP}} \in \{2,4,8,16,32\}$ for lcp_support_tree2

Any BPS provides the following methods:

• find_open(i), find_close(i),    enclose(i), rr_enclose(i,j), double_enclose(i),    excess(i), rank(i), select(i),

There are three BPS types:

Block sizes, rank support, and select support can be specified via template arguments.

Bitvector is interpreted as BPS.

//              0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
//              ( ( ( ) ( ) ) ( ) ( ( ( ) ( ) ) ( ) ) )
bit_vector b = {1,1,1,0,1,0,0,1,0,1,1,1,0,1,0,0,1,0,0,0};
bp_support_sada<> bps(&b); // <- pointer to b
cout << bps.find_close(0) << ", "
    << bps.find_open(3) << ", "
    << bps.enclose(4) << ", "
    << bps.double_enclose(13, 16) << endl;

Output:

19, 2, 1, 9

Bitvector is interpreted as BPS.

    //              0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
    //              ( ( ( ) ( ) ) ( ) ( ( ( ) ( ) ) ( ) ) )
    bit_vector b = {1,1,1,0,1,0,0,1,0,1,1,1,0,1,0,0,1,0,0,0};
    bp_support_sada<> bps(&b); // <- pointer to b
    for (size_t i=0; i < b.size(); ++i)
        cout << bps.excess(i)<< " ";
    cout << endl;
    cout << bps.rank(0) << ", "; // inclusive rank for BPS!!!
         << bps.select(4) << endl; 

Output:

1 2 3 2 3 2 1 2 1 2 3 4 3 4 3 2 3 2 1 0 
1, 4

Any RMQ provides operator(i, j) which returns the position of the min/max value in $[i..j]$

There are three RMQ types:

Underlying BPS and Min/Max can be specified via template parameters.

After construction the original sequence is not required any more:

    //                0 1 2 3 4 5 6 7 8 9 0
    int_vector<> v = {5,3,8,9,1,2,5,3,9,0,7};
    rmq_succinct_sct<> rmq(&v); // <- pointer to b
    util::clear(v);
    cout << "v.size() = " << v.size() << endl;
    cout << rmq(0, 10) << ", " << rmq(2, 7) << endl;

Output:

v.size() = 0
9, 4

• can be easily composed of this basic data structure
• Have a look into benchmarks/document_retrieval/src for an example

• Minimal monotone perfect hash functions (MMPHFs)
• Sparse CSAs/CSTs
• Fully-compressed SA
• LZ based indexes