- Big Data: Experiments on "massive" data
- Overview SDSL v2
- Example application for SDSL v2: Top-k frequent document retrieval
Overview
Experiments on "massive" data
Time performance of a single access/rank/select operation depends on
- Basic rank operation on 64-bit word:
- BW: SWAR (SIMD Within A Register)
- BLT: use popcount CPU instruction
- Virtual address space translation:
- no HP: Use standard 4 kiB pages
- HP: Use 1GiB pages (hugepages)
- Data structure design:
- RANK-V:
rank_support_v<>25% overhead on top ofbit_vector - RANK-1L
interleaving bitvector data and rank data (
bit_vector_il<>)
- RANK-V:
Experiments on "massive" data
"BV access"
is the baseline of accessing a random bit of a bit_vector.
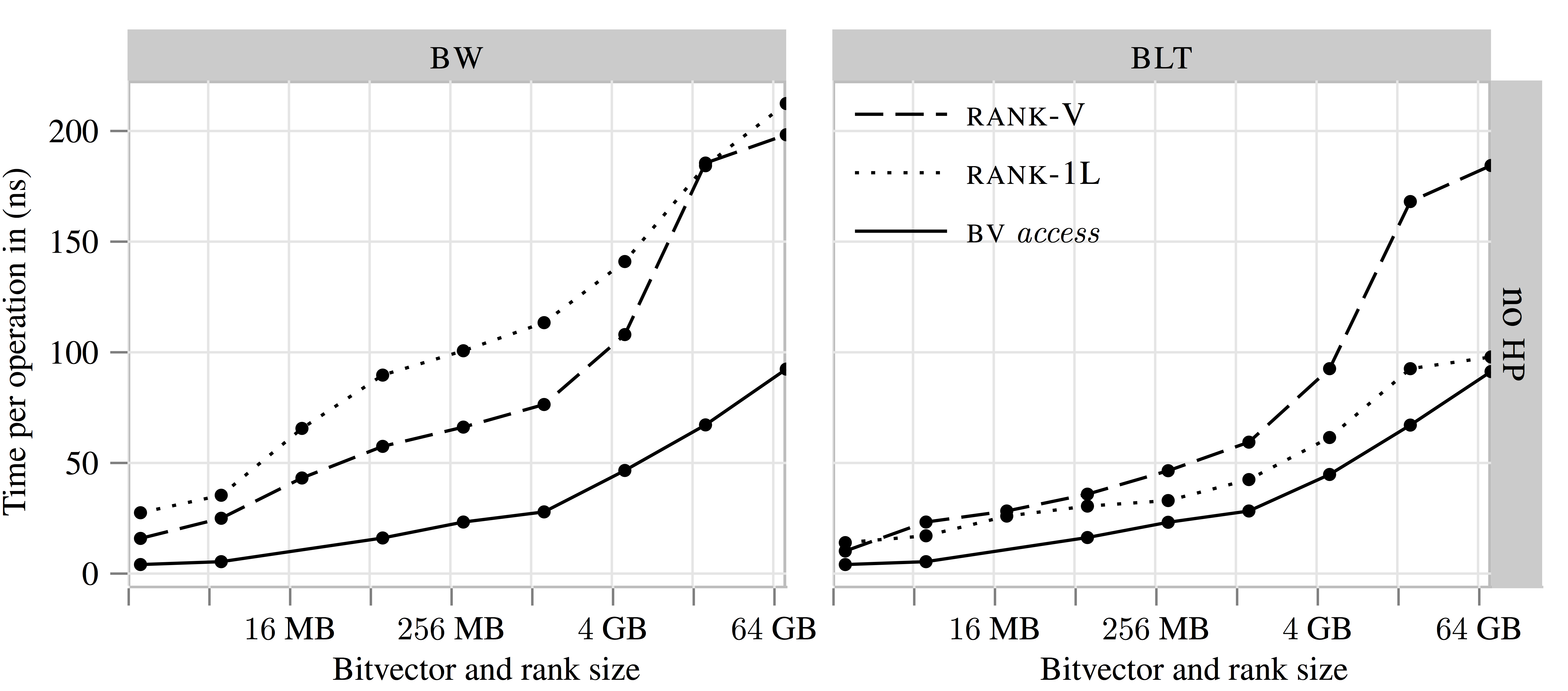
Experiments on "massive" data
"BV access"
is the baseline of accessing a random bit of a bit_vector.
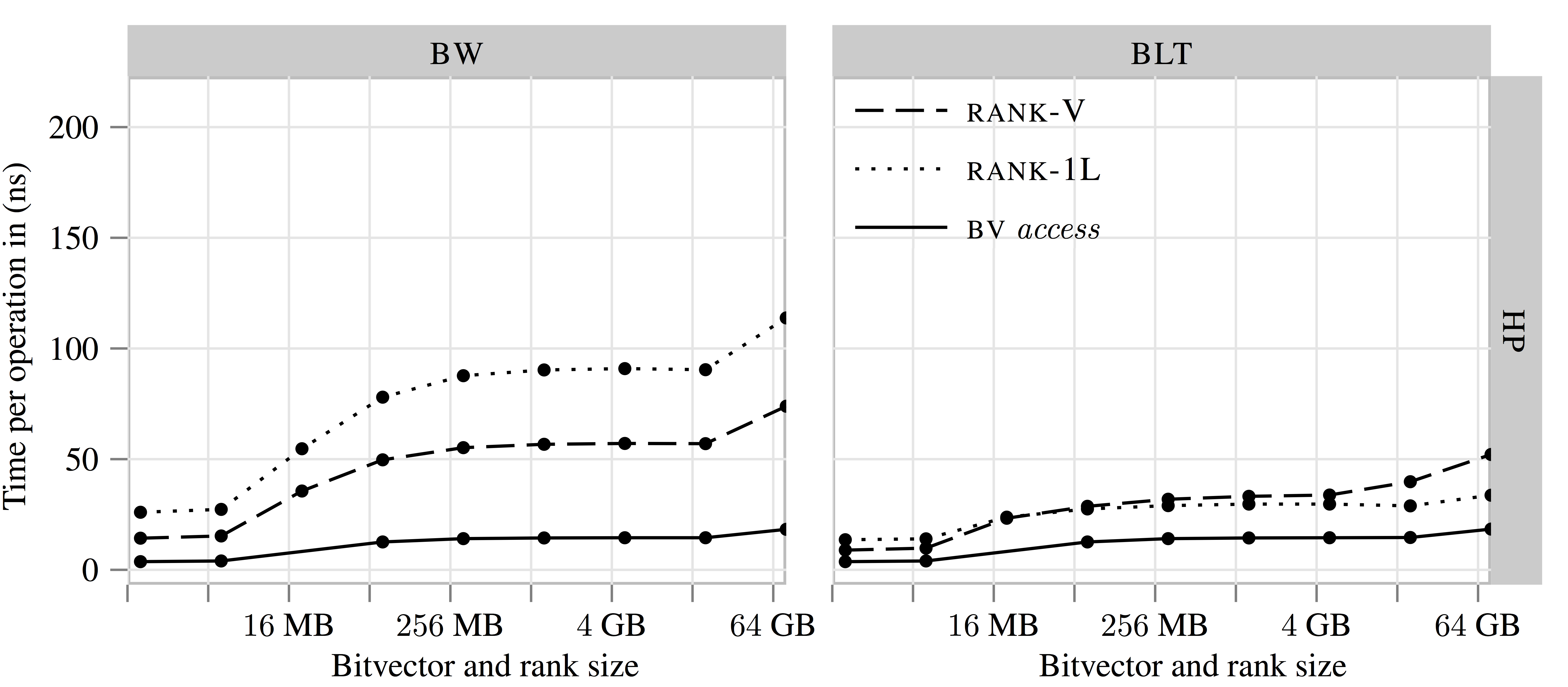
Experiments on "massive" data
Performance of binary search select (SEL-BS*),
select_support_mcl<> (SEL-C)
and Vigna's solutions in Sux
SEL-V9 and SEL-VS
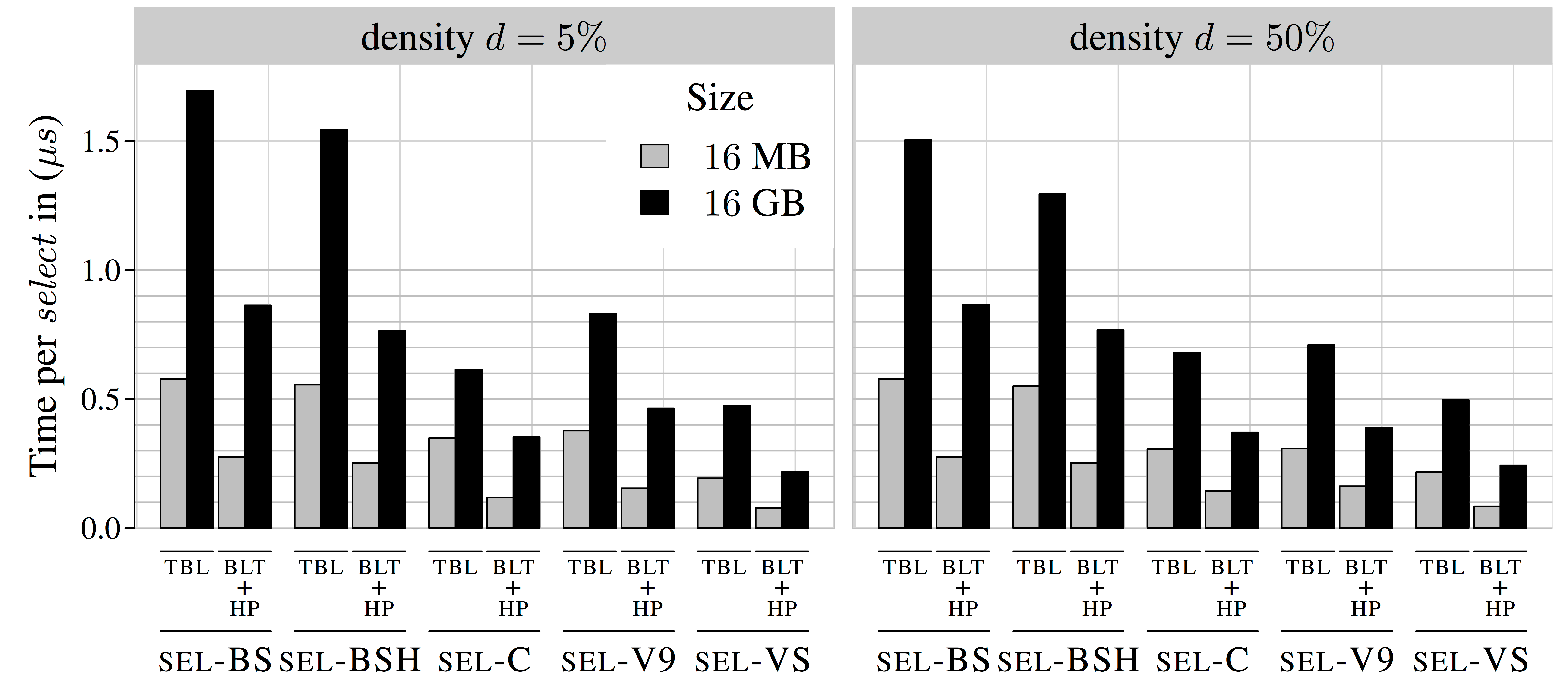
Experiments on "massive" data
Space breakdown for
rrr_vector<K>
with varying block size.

Experiments on "massive" data
Runtime for
rrr_vector<K>
with varying block size.
Experiments on "massive" data
Time-space trade-offs of different FM-indexes.

Experiments on "massive" data
Construction of a cst_sct3<> for WEB-5G (no HP)
Experiments on "massive" data
Construction of a cst_sct3<> for WEB-5G (HP)
..implements 40 research papers. We stand on the shoulders of giants
SDSL v2: Data Structures Overview
- Integer Vectors (IV)
- Bitvectors (BV)
- Rank Support(RS)
- Select Support (SLS)
- Wavelet Trees (WT=BV+RS+SLS)
- Compressed Suffix Arrays (CSA=IV+WT)
- Longest Common Prefix (LCP) Arrays
- Balanced Parentheses Supports (BPS)
- Compressed Suffix Trees (CST=CSA+LCP+BPS)
- Range Min/Max Query (RMQ) Structures
- ...
- Top-k Frequent Document Structures
SDSL v2: Release Notes
- ..simplifies the usage of the library
- ..features integer-alphabet versions of all indexes
- ..contains a unified implementation of pointer based WTs
- ..introduces a Hu-Tucker-shape strategy for WTs
- ..facilitates the user to switch between semi-external and in-memory construction
- ..enables the use of 1 GB hugepages
- ..provides more sophisticated visualizations (resource graph/memory breakdowns)
- ..includes a tutorial slides set and a new cheatsheet
- ..comes with a set of fully automated benchmarks
- ..includes a comprehensive test suite
Wavelet trees (WTs)
#include <sdsl/wavelet_trees.hpp>
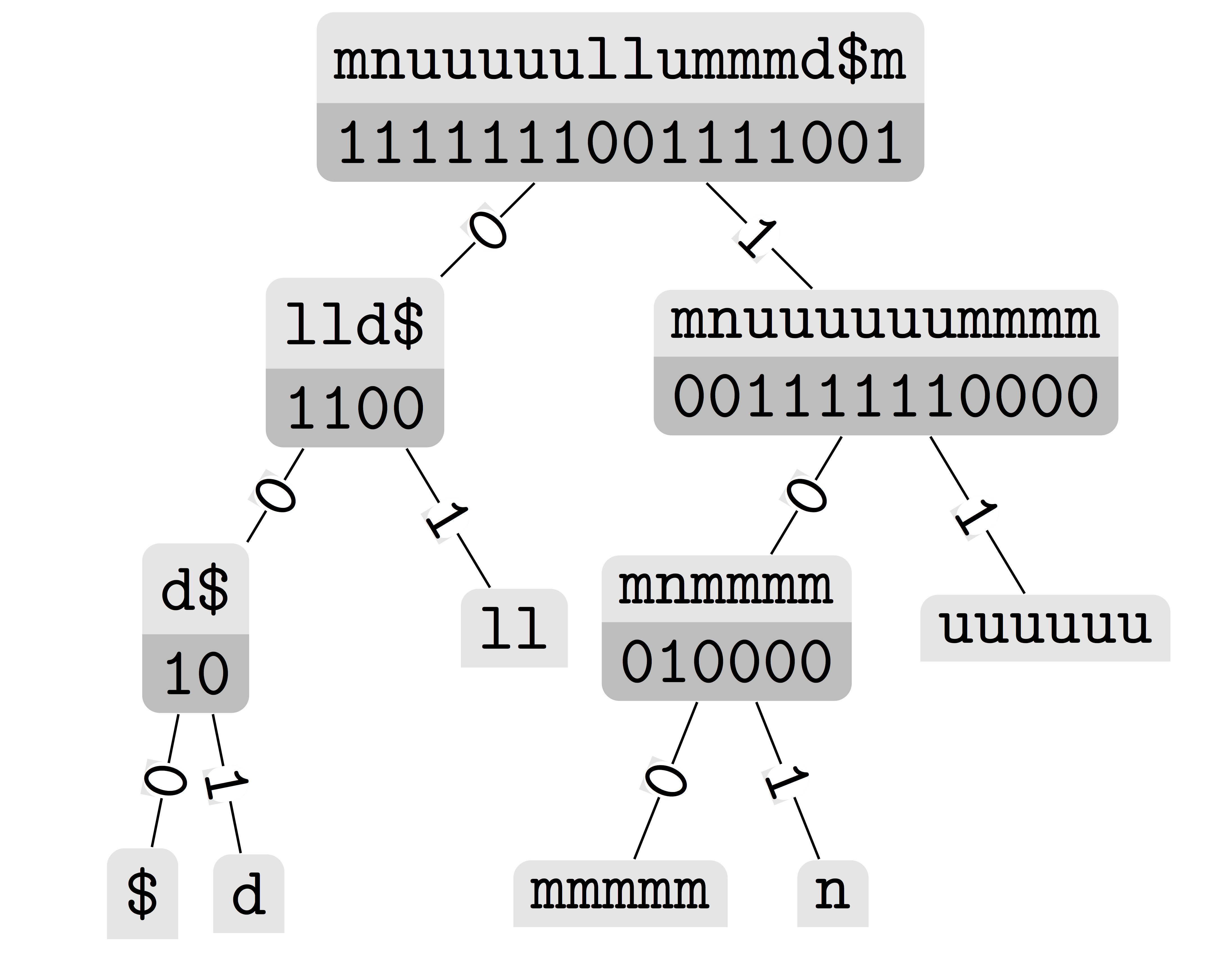
Wavelet trees (WTs) - Overview
wt_pc<..>: Prefix code wavelet tree (parametrizable with shape, bitvector, rank, selects, alphabet) using . Shape specializations:wt_blcd<..>: Balanced-shaped WTwt_huff<..>: Huffman-shaped WTwt_hutu<..>: Hu-Tucker-shaped WTwt_int<..>: Balanced-shaped WT for large alphabets (parametrizable with bitvector, rank, selects)wt_rlmn<..>: Run-length WT (parametrizable with bitvector, rank, select, and the underlying WT)
Note:
-
wt_pcandwt_rlmncan be parametrize to work on byte or integer alphabets. -
wt_blcd,wt_hutuandwt_intare order preserving WTs.
Wavelet Trees (WTs) - Example
Build a byte-alphabet Hu-Tucker-shaped WT
(order preserving) for a byte sequence
and call lex_count.
wt_hutu<rrr_vector<63>> wt;
construct_im(wt, "情報学 研究所", 1);
cout << wt << endl;
auto t1 = wt.lex_count(0, wt.size(), 0x80);
auto t2 = wt.lex_count(0, wt.size(), 0xbf);
cout << "# of chars : " << wt.size() << endl;
cout << "# of UTF-8 symbols: " << get<1>(t1)+get<2>(t2) << endl;
Output:
情報学 研究所 # of bytes : 19 # of UTF-8 symbols: 7
Wavelet Trees (WTs) - Example
Build an integer-alphabet balanced WT (order preserving) for a integer sequence and do a range search (index range = [1..5], value range=[4..8]).
wt_int<rrr_vector<63>> wt;
construct_im(wt, "6 1000 1 4 7 3 18 6 3", 'd');
auto res = wt.range_search_2d(1, 5, 4, 18);
for ( auto point : res.second )
cout << point << " ";
cout << endl;
Output (index/value pairs):
(3,4) (4,7)
Compressed Suffix Arrays (CSAs)
#include <sdsl/suffix_arrays.hpp>
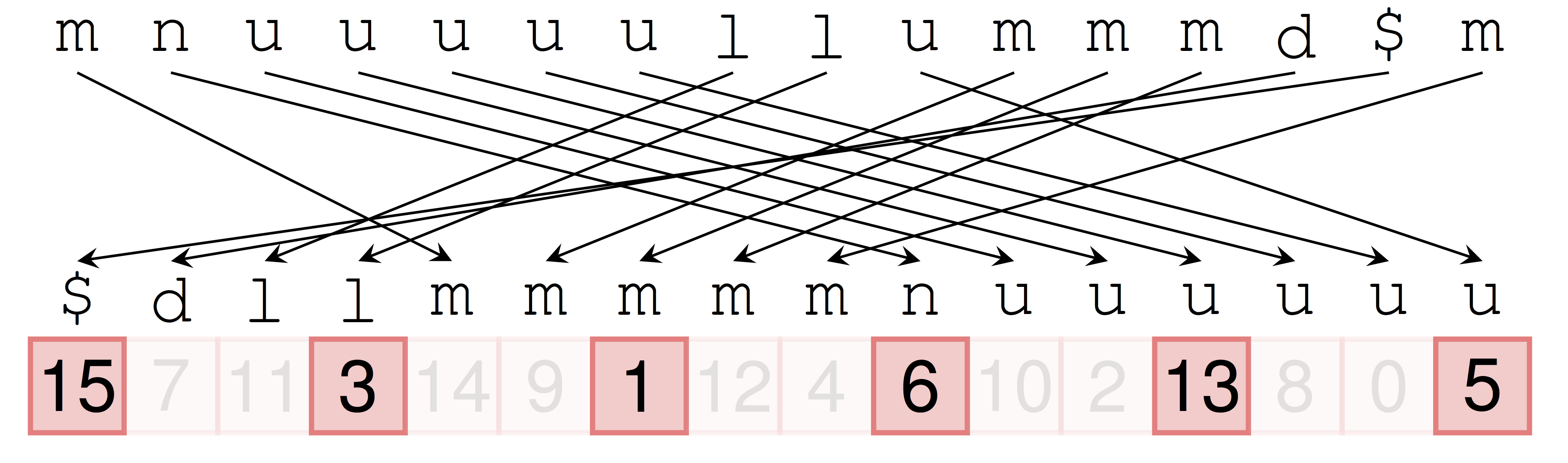
Compressed Suffix Arrays (CSAs) - Overview
Any CSA provides the access method (operator[]) and
the following members:
-
psi,lf,isa,bwt,text,L,F,C,char2comp,comp2char
There are three CSA types:
csa_bitcompressed<..> |
Based on SA and inverse SA (ISA) stored in an int_vector<>.
|
csa_sada<..> |
Based on $\Psi$-function. $\Psi$ is stored in an vector. The vector
type is a template parameter and enc_vector per default.
|
csa_wt<..>
|
Based on a WT over the Burrows-Wheeler-Transform (BWT);
aka FM-Index. WT is parametrizable, default WT is
wt_huff.
|
SA and ISA sampling density, alphabet strategy and the SA value sampling strategy can be specified via template arguments.
Compressed Suffix Arrays (CSAs) - Example
Build an byte-alphabet CSA in memory
(0-symbol is appended!). Output size,
alphabet size, and extracted text in
[0..csa.size()-1].
csa_bitcompressed<> csa; construct_im(csa, "abracadabra", 1); cout << "csa.size(): " << csa.size() << endl; cout << "csa.sigma : " << csa.sigma << endl; cout << csa << endl; cout << extract(csa, 0, csa.size()-1) << endl;
Output:
csa.size(): 12 csa.sigma : 6 11 10 7 0 3 5 8 1 4 6 9 2 abracadabra
Compressed Suffix Trees (CSTs)
#include <sdsl/suffix_trees.hpp>
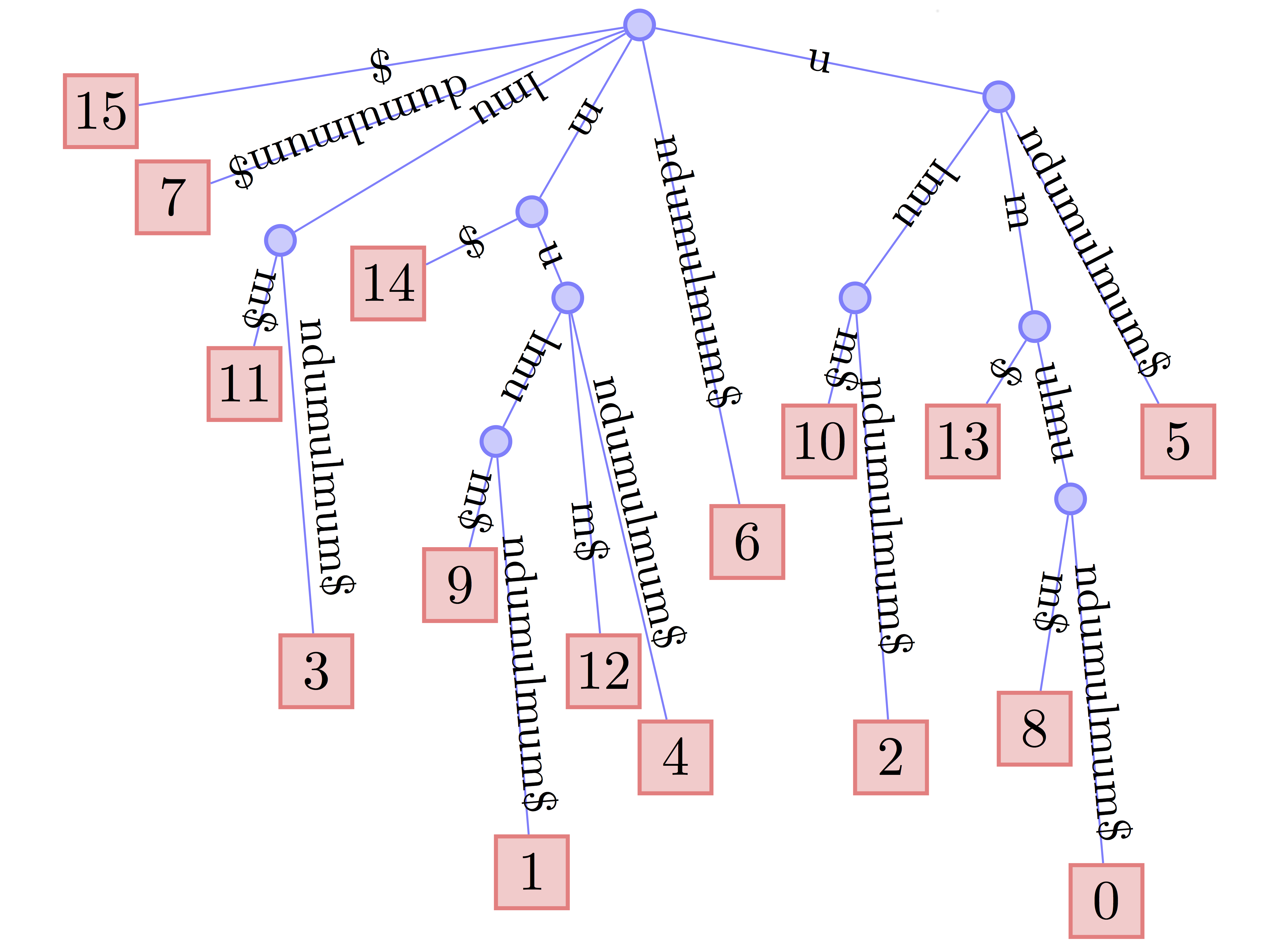
Compressed Suffix Trees (CSTs) - Overview
Any CST contains members csa and lcp
and provides the following methods:
-
nodes(),root(),begin(),end(),begin_bottom_up(),end_bottom_up() -
size(v),is_leaf(v),degree(v),depth(v),node_depth(v),edge(v,d),lb(v),rb(v),id(v),inv_id(i),sn(v) -
select_leaf(i),node(lb,rb) -
parent(v),sibling(v),lca(v,w),select_child(v,i),child(v,c),sl(v),wl(v,c),leftmost_leaf(v),rightmost_leaf(v)
There are two CSA types:
cst_sct3<..> |
Interval based node representation. |
cst_sada<..> | Node represented as position in balanced parentheses sequence. |
The underlying CSA, LCP array and the balanced parentheses structure can be specified via template arguments.
Compressed Suffix Trees (CSTs) - Example
Use a CSTs to calculate the $k$-th order entropy of a integer sequence.
cst_sct3<csa_wt<wt_int<rrr_vector<>>>> cst;
int_vector<> data(100000, 0, 10);
for (size_t i=0; i < data.size(); ++i)
data[i] = 1 + rand()%1023;
construct_im(cst, data);
cout << "cst.csa.sigma: " << cst.csa.sigma << endl;
for (size_t k=0; k<3; ++k)
cout << "H" << k << " : " << get<0>(Hk(cst, k)) << endl;
Output:
cst.csa.sigma: 1024 H0(data) : 9.99038 H1(data) : 6.52515 H2(data) : 0.0940461
Top-k frequent document retrieval (Space)
Implementation by Culpepper et al. (ESA 2010)
| Test case | SADA | GREEDY | QPROBING |
|---|---|---|---|
| PROTEINS | 870 (15.4) | 217 (3.84) | 217 (3.84) |
Faithful implementation using SDSL
| Test case | SADA | GREEDY | QPROBING |
|---|---|---|---|
| PROTEINS | 148 (2.62) | 162 (2.87) | 162 (2.87) |
| ENWIKI-SML | 199 (3.07) | 130 (2.01) | 130 (2.01) |
| ENWIKI-BIG | 23,914 (2.80) | 27,043 (3.17) | 27,043 (3.17) |
Space breakdown (GREEDY/QPROBING)
Space breakdown (SADA)
Space breakdown (SADA)
<Thank You!>